EWMA

EWMA Algorithm

میانگین متحرک موزون نمایی (Exponentially Weighted Moving Average) توسط روبرتز (1959) معرفی شد. این روش به عنوان الگوریتم شناسایی طغیان توسط برخی از محققین از جمله رابینسون و هو (1978)، هانتر (1986) و والدمن (1986) بکار گرفته شد و ویژگی‌های آن مورد ارزیابی قرار گرفت. اگرچه تا پیش از این نیز، ویژگی‌های بهینه این روش به عنوان یک روش سری زمانی، در کنترل کیفیت فرآیندهای تولید شناخته شده بود، اما به عنوان یک ابزار توسط تحلیل‌گران کنترل کیفیت تا حد زیادی نادیده گرفته می‌ شد. EWMA در زمان t بر اساس آماره

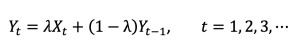
تعریف می‌ شود که X_t تعداد بیماران (موردها) است و λ پارامتر وزن دهی یا مقدار ثابت هموارسازی است و مقادیر مختلف بین 0 ≤ λ ≤ 1 را شامل می شود. در رابطه بالا مقدار شروع  Y₀ ، EWMA برابر با مقدار تحت کنترل μ₀ در نظر گرفته می شود. گاهی از میانگین داده‌های اولیه، به عنوان مقدار تحت کنترل  استفاده می شود، لذا

از آنجایی که EWMA می تواند به عنوان میانگین وزنی تمام مشاهدات گذشته و کنونی در نظر گرفته شود، نسبت به فرض نرمال بودن حساس و در شناسایی تغییرات کوچک بسیار موثر است؛ بنابراین یک نمودار کنترلی ایده‌آل برای مشاهدات منفرد است. نمودار کنترل EWMA با رسم Y_t در مقابل زمان ساخته می شود. فرض کنید σ انحراف معیار X_t باشد، اگر Y_t بزرگتر از سطح آستانه هشدار باشد، هشدار وقوع طغیان اعلام خواهد شد.  سطح آستانه هشدار یا حد بالای کنترل EWMA عبارت است از

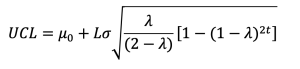
که با گذشت زمان و بزرگتر شدن مقدار t، عبارت [1-(1-λ)^2t]  به یک نزدیک می‌شود. لذا پس از اینکه نمودار کنترل EWMA برای چندین دوره زمانی اجرا شد، حد بالای کنترل به مقدار پایدار

خواهد رسید. با این حال، اکیداً توصیه می ‌شود که از حدود کنترلی دقیق برای مقادیر کوچک t استفاده شود زیرا این کار با بالا نگه داشتن حساسیت، عملکرد الگوریتم را در تشخیص یک فرآیند خارج از کنترل بهبود می بخشد. انتخاب مقادیر مربوط به پارامترهای L و λ از طریق میانگین طول اجرا، بر نحوه عملکرد الگوریتم EWMA تاثیرگذار است. مطالعات تئوری متعددی در مورد ویژگی‌های مربوط به میانگین طول اجرا نمودار کنترل EWMA انجام شده است؛ برای مثال، مقاله لوکاس و ساکوچی (1990) جداول یا نمودارهای متوسط طول اجرا را برای محدوده ای از مقادیر L ، λ ارائه می دهند. آنچه که از مطالعات متعدد به طور کلی مشهود است، آن است که مقادیری از L که در بازه‌ی 2.60 ≤ L ≤ 2.80 و مقادیری از λ که در بازه‌ی 0.05 ≤ λ ≤ 0.25 قرار دارند، عملکرد خوبی دارند و
λ=0.05, λ=0.10, λ=0.20  انتخاب ‌های محبوب هستند. یک قانون کلی خوب، استفاده از مقادیر کوچکتر λ برای تشخیص تغییرات کوچکتر است.

منابع:

Roberts S. Control chart tests based on geometric moving averages. Technometrics. 2000;42(1):97-101.

Hunter JS. The exponentially weighted moving average. Journal of quality technology. 1986;18(4):203-10.

Lucas JM, Saccucci MS. Exponentially weighted moving average control schemes: properties and enhancements. Technometrics. 1990;32(1):1-12.

Robinson P, Ho TY. Average run lengths of geometric moving average charts by numerical methods. Technometrics. 1978;20(1):85-93.

Waldmann KH. Bounds for the distribution of the run length of geometric moving average charts. Journal of the Royal Statistical Society: Series C (Applied Statistics). 1986;35(2):151-8.

Montgomery DC. Introduction to statistical quality control: John Wiley & Sons; 2020.

زارعی، بشرا و همکاران (1401). طراحی مجموعه ابزارهای ارزشیابی الگوریتم‌های شناسایی طغیان در کشف بهنگام انواع اپیدمی‌های تک منبعی و پیش‌رونده. پایان نامه دکترای تخصصی. دانشگاه علوم پزشکی همدان.