CUSUM Algorithm

Guide to using CUSUM algorithm for count data based on Poisson distribution

Arguments	Description
Reference Value (k)	The reference value
Decision Interval (H)	Decision making interval help: Hint: A decision interval denoted by H will be used to indicate the occurrence of out-of-control situations. This value is usually considered as H=5.
Range of Data:	Determines the desired time period to be evaluated.
Start Year	Enter the start year of the data.
Start Month	Enter the starting month of the data.
Frequency	If the data scale is weekly, select the number 52 and if the data scale is monthly, select the number 12.
Choose xlsx File	In this section, upload the data file. The data structure should be according to the desired sample.

CUSUM Algorithm
One of the control charts for detecting small changes is the Cumulative Sum (CUSUM), which was introduced by Page (1954) as a method for controlling continuous data. The CUSUM chart uses cumulative sums of deviations from the sample values to the target value, directly utilizing all the information in the sequence of sample values. Suppose the sample size is n ≥1 and the mean of the first j samples is . If the target value for the mean of this process is , then the CUSUM chart is created by plotting :

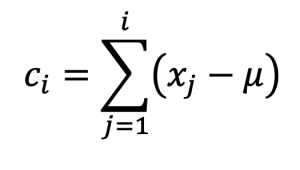
against the sample number i. The quantity is called the cumulative sum, which also includes the i-th sample. Many random phenomena rely on counting the occurrences of specific events within a given timeframe or location. For instance, this includes tracking the number of school absences per term, monthly asthma attacks per 100 children, or annual falls in an aged care facility. This statistical method is both accurate and powerful, but it assumes that the variable representing the number of occurrences follows a Poisson distribution, where the variance is equal to the mean. The parameter ; denotes the reference value and is typically chosen to lie between the desired target value and the out-of-control value, , that requires prompt identification. In the CUSUM method, which is based on the Poisson distribution, the value of 'k' is calculated using the following equation::

When this assumption is not met, it is advisable to use the alternative number model based on the negative binomial distribution, which is less powerful but more tolerant.

REFERENCE

MONTGOMERY, Douglas C. Statistical quality control. New York: Wiley, 2009.‏